今日の例題 「 非定常時系列(季節変動を含む)のモデル 」
- 解説: ARIMA(積分混合自己回帰移動平均過程)
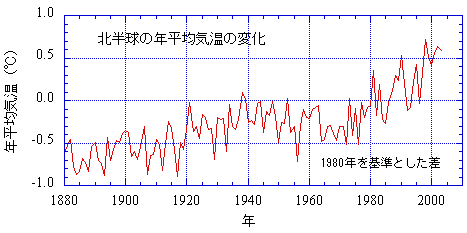
平均値が大きく変動する(トレンドを含む)非定常な時系列は,階差(差分)を取ることで定常とみなせる場合がある。階差を取ることはZ変換を使って,次のように表現できる。
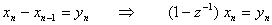
q回階差を取る場合は,
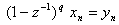
となる。得られた階差時系列が定常と見なせるなら,それはARMAモデルで表現できるはずである。
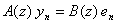
したがって,元の時系列は,
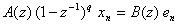
と表現できる。これはARMAで表現できる定常時系列を積分(階差(差分)の逆操作)したものと見なせることから,ARIMA(AutoRegressive Integrated Moving Average)モデルと呼ばれる。また,元の時系列に明確な周期の変動(季節変動と呼ぶ)が含まれる場合,すなわち,たとえば月ごとに記録したデータのような場合には,1年ごとの周期(12の周期)が自ずと含まれるから,この周期の変動を予め除去しておくことも有効であろう。p 周期の変動が含まれるなら,
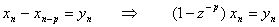
というように,p 周期の差分をとった時系列について考えるのである。これらすべてを組み合わることによって,トレンドと季節変動を含む非定常時系列に対する一般的なモデルが構築できる。
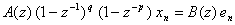
なお,時系列を予測するにおいては,MAの部分は入力がわからないと利用できないから,階差と季節変動除去をしたあとの時系列についてARのみの過程としてモデル化し,
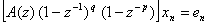
上の式の左辺の括弧内全体を,改めて1つのAR過程(単位円状の極も許容するもの)と見立てて,予測式を作ればよい。 - 例題プログラム: [ arima.m ]
次のプログラムでは,まず,適当に与えたARMA過程をもとに,1回の積分にあたるトレンドと,p=12の周期の季節変動を含むようなサンプル時系列を生成している。そして改めて,そのサンプル時系列について1回階差をとり,さらにp=12周期の差分をとって,ほぼ定常な時系列とし,ARMAモデルをあてはめて,内包されていたARMA過程が回復できているかどうか(スペクトルを比較して)チェックしている。
オリジナルのプログラムは, こちらから,ダウンロード% -------------------------------
% ARIMA 過程の同定
% -------------------------------
%
N = 240; % ある ARIMA過程(ドリフトと年変動を含む) を想定
a = [1 -0.763 0.624]; % A(z)
az = [1 -1]*[a 0;0 a]; % (1-z^(-1)) A(z)
azz = [az zeros(1,12-length(az)) -1*az] % (1-z^(-12))(1-z^(-1)) A(z)
b = [1 0.13 0.02]; % B(z)
%
% % (1-z^(-12))(1-z^(-1)) A(z)*Xn = B(z)*En
%
x = filter(b,azz,5*randn(240,1)); % サンプル時系列生成
subplot(421);plot(x); axis([0 240 -1000 1000]);legend('sample Xn',3)
fy = freqz(b,a,N);
subplot(422);semilogy(abs(fy));axis([0 120 1 100]);legend('buried ARMA')
%
y=x(2:N)-x(1:N-1); % 階差時系列
subplot(412);plot(y); axis([0 240 -200 200]);legend('difference Yn= Xn+1-Xn',3)
%
z=y(13:N-1)-y(1:N-13); % 年変動除去
subplot(413);plot(z); axis([0 240 -100 100]);legend('difference Zn= Yn+12-Yn',3)
%
% 階差時系列を AR過程 で同定
%
ai = aryule(y,20); % Yule-Walker法 /次数(20)
fy = freqz(1,ai,N);
subplot(427);semilogy(abs(fy));axis([0 120 1 100]);legend('spectrum of Yn',2)
%
% 年変動除去後の時系列を ARMA過程 で同定
%
ai = aryule(z,30); % Yule-Walker法 /次数(30)
hai=impz(1,ai,N); % インパルス応答
[bs,as] = stmcb(hai,2,2,10) % 次数(4,4); 10 iterations (Steiglitz-McBride法)
fz = freqz(bs,as,N);
subplot(428);semilogy(abs(fz));axis([0 120 1 100]);legend('recovered ARMA')
- 演習: 例題プログラムを実行してみよう
まず実行してみて,このプログラムの内容をよく理解してください。
- もともとのARMA係数や推定する次数を変えるなど,いろいろと試してみてください。