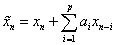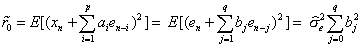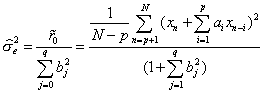今日の例題 「 ＡＲモデルからＡＲＭＡモデルへ 」
- 解説： ＡＲＭＡ（自己回帰移動平均）モデル
自己回帰移動平均モデル（ARMAモデル）は，
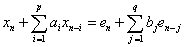
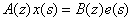ここで， 
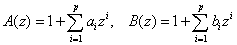
非常に次数の多く必要なARモデルを，より少ないパラメーターで表現する方法と見ることができる。
ARMAモデルの同定法の1つに，まず，次数を十分大きく取ったAR過程としてモデル化し，それから求めた推定インパルス応答に対して，ARMAモデルをあてはめるという方法がある。与えられたインパルス応答に対してARMAモデルをあてはめる具体的な方法として，MATLABには，係数比較にもとづくProny法と，繰り返し計算によって最適な係数を求めるSteiglitz-Mcbride法（繰返し計算の初期値としてProny法の結果が利用される）が提供されている。 - 例題プログラム： [ arma.m ]
次のプログラムでは，適当に与えたARMA過程について，サンプル時系列を生成し，その時系列から逆にARMAモデルの同定を行って，与えたモデルに一致するかどうか調べるプログラムである。まず与えたサンプル時系列に対して，次数の大きなARモデル（今の場合30次）をYule-Walker法（aryule）であてはめて，それから生成したインパルス応答（impz）に対して，Prony法（prony）とSteiglitz-Mcbride法（stmcb）によって，ARMAモデルをあてはめている。
オリジナルのプログラムは， こちらから，ダウンロード% -----------------------------------
% AR model から ARMA model へ
% ----------------------------------
%
% ある ARMA過程 を想定して
%
Fs = 1000;
N = 500;
a = [1 -1.31 1.44 -1.10 0.84];
b = [1 0.13 0.02 0.11 0.04];
h = impz(b,a,N); % そのインパルス応答
subplot(521);plot(h)
legend('given impulse response')
%
f = freqz(b,a,N); % その周波数応答
subplot(522);semilogy(abs(f));
axis([0 500 1 100]);legend('given frequency response')
%
x = filter(b,a,1*randn(1024,1)); % サンプル時系列生成
subplot(523);plot(x);
axis([0 1000 -20 20]);legend('sample')
[pxx,fr] = psd(x,256,Fs,hanning(256),128); % FFT法によるスペクトル推定
subplot(524);semilogy(fr,sqrt(pxx));
axis([0 500 1 100]);legend('FFT spectrum')
%
% AR過程（次数無限大）として同定
%
ai = aryule(x,30); % Yule-Walker法 ／次数(30)
%
hai=impz(1,ai,N); % インパルス応答
subplot(525);plot(impz(1,ai,N))
legend('AR model')
f = freqz(1,ai,N);
subplot(526);semilogy(abs(f));
legend('AR model');axis([0 500 1 100])
%
% ARモデル -＞ ARMAモデル
%
% ARMAモデル （prony法）
%
[bci,aci] = prony(hai,4,4) % 次数(4,4)
subplot(527);plot(impz(bci,aci,N));
legend('ARMA (prony)')
f = freqz(bci,aci,N);
subplot(528);semilogy(abs(f));axis([0 500 1 100])
%
% ARMAモデル （Steiglitz-McBride法）
%
[bs,as] = stmcb(hai,4,4,10) % 次数(4,4) 繰返し計算10回
subplot(529);plot(impz(bs,as,N));
legend('ARMA (Steiglitz-McBride)')
f = freqz(bs,as,N);
subplot(5,2,10);semilogy(abs(f));axis([0 500 1 100])
- 演習： 例題プログラムを実行してみよう
まず実行してみて，このプログラムの内容をよく理解してください。
うまくモデル化できているでしょうか？- 推定するARMAの次数をいろいろ変えてみてください。
- はじめに想定しているARMAモデルの係数をかえてみてください。
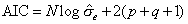
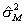は，予測誤差の分散（推定値）である。なお，予測誤差の分散を求める方法は，下記の補足解説を参照しなさい。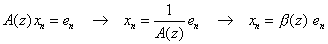
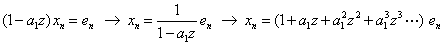
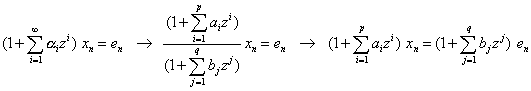
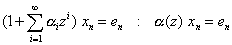
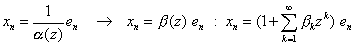
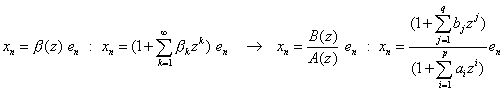
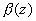が与えられた状況で，次の式でｚの等べき項を比較すればよい。
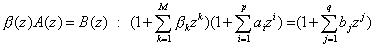
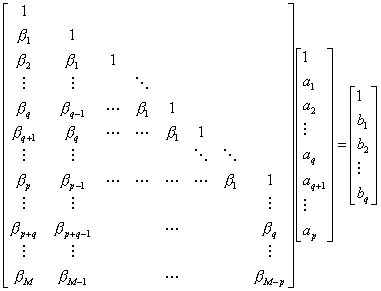
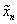とおく。
